Complete Guide: Delta

Options Delta is the most common and discussed Option Greeks, and for good reason. Delta is the directional component of option profitability and crucial for understanding options profitability. Delta is always dynamic, which means it changes with respect to other factors, including price, implied volatility and time.

1. What is Options Delta?

Delta can be understood from both a mathematical and an intuitive perspective:

• Mathematical Definition: Delta is formally defined as the first derivative of the Black-Scholes option pricing model with respect to price change. In simpler terms, it measures how an option price will move given a $1 move in the underlying stock price. Since options rarely move one-for-one with a stock, Delta allows us to approximate how the option price will change given a change in the stock price.
• Intuitive Understanding: Delta provides a sense of how your options positions will move around as stock prices move around. It helps traders process the directional sensitivity of their option contracts.

2. How Traders use Delta

Measuring Option Price Change per Underlying Price Change:

• Delta quantifies the expected change in an option's price for every $1 movement in the underlying asset.
• For example, if an option has a Delta of 30 (or 0.3 in decimal form), it means the option price is expected to move by 30 cents for every $1 move in the stock. As each option contract typically represents 100 shares, a 30 Delta would mean a $30 change per $1 stock move on a per-contract basis. If the stock moves $1, a $4.00 option price would be expected to change to $4.30 or $3.70, depending on the direction of the stock move and the type of option, all else being equal.

Approximate Probability Gauge:

• Delta can serve as an approximate probability gauge, specifically estimating the probability that an option will expire in-the-money (ITM).
• For premium sellers, who generally want options to expire out-of-the-money (OTM), Delta helps gauge the approximate probability of success (i.e., expiring OTM). If a short put strategy has a Delta of 30, it suggests an approximate 30% probability that the option will expire in-the-money, meaning an approximate 70% probability of success for the seller. This can be useful at trade entry.
• Share Equivalent (Directional Bias/Exposure):
  • Delta can also be used as a share equivalent to measure your directional bias or exposure in a portfolio.
  • This interpretation helps traders understand how a position will feel in terms of directional exposure, even if the contract is for 100 shares. For instance, a position with a Delta of 40 will feel like owning 40 shares of stock.
  • Dollar Delta reflects the options delta multiplied by the share price, and is a further useful portfolio management tool. A 40 Delta Call option on a $50 stock gives the trader $2,000 of bullish investment.

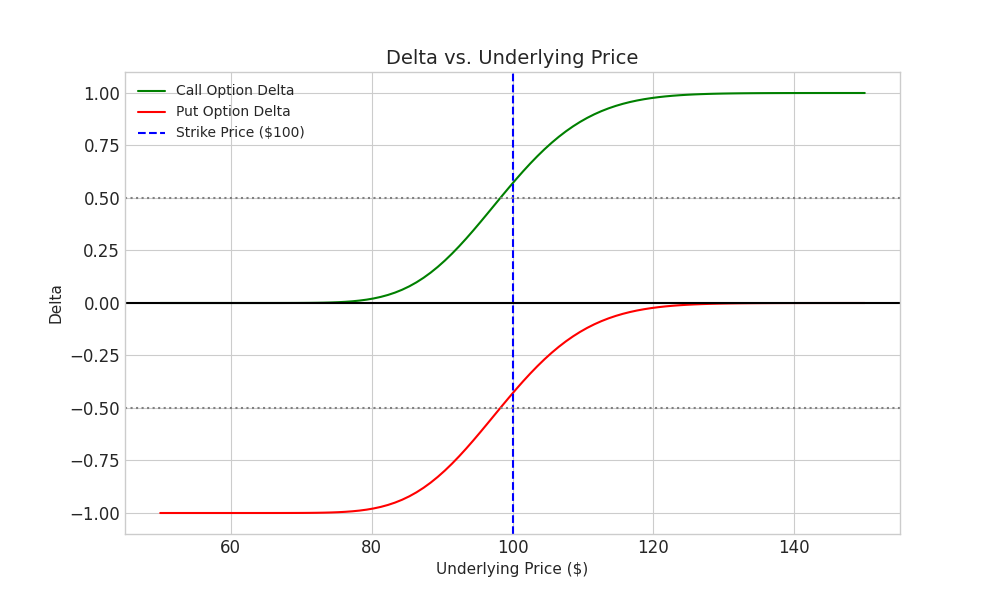
3. Delta's Directional Nature: Positive and Negative Delta

The sign of Delta indicates the directional bias of an option position:

• Positive Delta:
  • Bullish positions are associated with positive Delta.
  • Examples include long calls and short puts. These positions generally profit when the underlying stock price increases.
  • A long call has positive Delta because if the stock rallies, its Delta will increase, and if the stock falls, its Delta will decrease.
  • A short put benefits from the stock moving higher and is considered a bullish position.
• Negative Delta:
  • Bearish positions are associated with negative Delta.
  • Examples include long puts and short calls. These positions generally profit when the underlying stock price decreases.
  • A long put has negative Delta because if implied volatility rises, its Delta will move lower, meaning it becomes more negative, increasing the likelihood of expiring in the money.

4. Delta's Impact on Returns

Delta is one of the three primary ways to make money when trading options (the others being Theta and Vega).

• For premium sellers, an advantage can be found by selling bigger Delta options (e.g., a 45 Delta over a 35 Delta). This is because higher Delta options carry higher premiums, leading to greater profit potential.
• Trade-off: However, selling higher Delta options means you are accepting a lower probability of profit because Delta also represents the probability of expiring in-the-money. For example, selling a 45 Delta option means a 55% probability of max profit, whereas selling a 35 Delta option implies a 65% probability of max profit.
• Simply, a higher delta option has more premium and is more expensive.

5. Managing Risk with Delta

Given the inherent randomness and unpredictability of the stock market, controlling directional risk (Delta risk) is paramount.

• Controlling Size: The most important way to control Delta-related risk is to control your position size. Whether at the individual position level or the overall portfolio level, ensuring your Delta exposure is manageable is crucial. Small position sizing allows traders to manage risk, build profits, act strategically, and analyse objectively.
• Staying small with position sizing (e.g., 1-5% of total account net liquidating value for defined risk, 3-10% for undefined risk) helps give probabilities a chance to work over time.

6. Delta in the Context of Other Options Greeks

Delta is interconnected with other Greeks, which provide further insights into its behaviour:

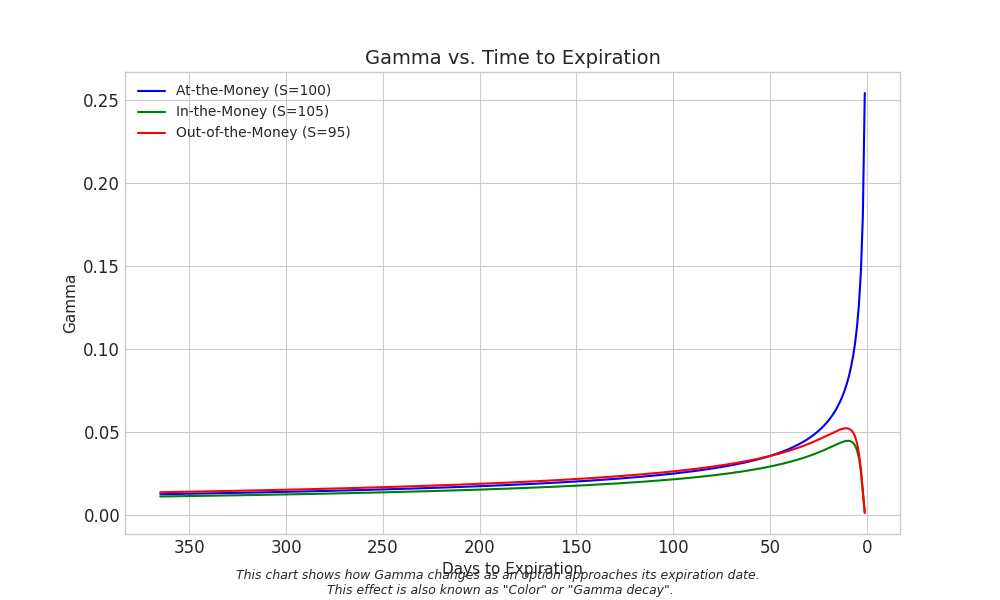
• Gamma: Gamma is a second derivative of the Black-Scholes model that measures how Delta itself changes as the stock price changes. While Delta is like the "speed" of an option, Gamma is its "acceleration," indicating how rapidly that speed (Delta) will change. For premium sellers, who are usually negative Gamma, this means their directional biases can strengthen, weaken, or even flip as the underlying moves. Gamma naturally rises sharply closer to expiration.

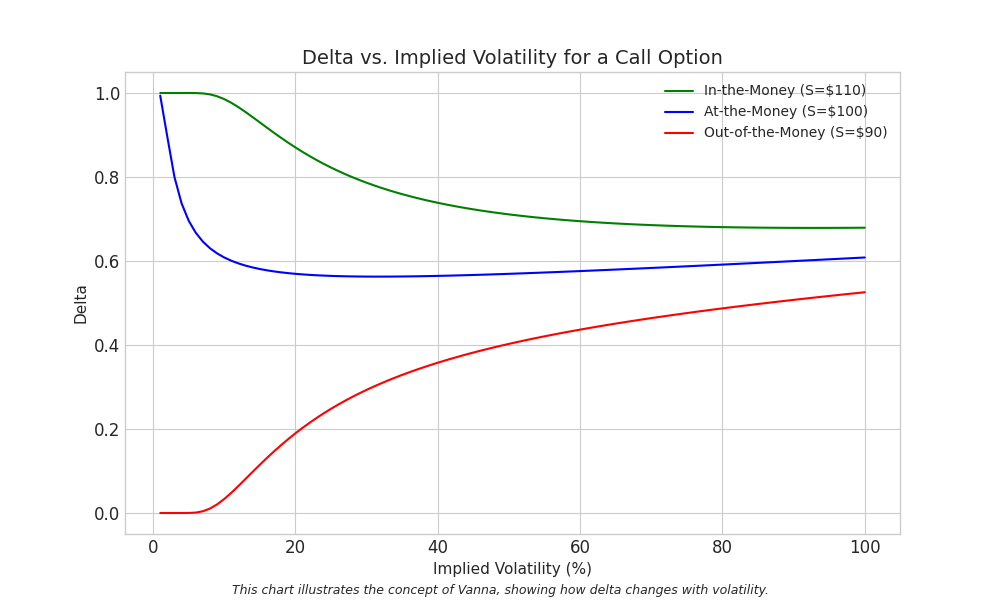
• Vanna: Vanna is another second-order Greek that measures how Delta changes when implied volatility changes. This gives another unique perspective on how Delta, the directional metric, can be impacted by shifts in market volatility. For instance, with long calls (positive Vanna), if implied volatility rises, their Deltas will also rise. For short puts (positive Vanna), a bullish move in the stock combined with contracting volatility can lead to Deltas shrinking, contributing to faster premium decay. Understanding Vanna helps appreciate the compounding effects of different Greeks on risk and profitability, especially for outlier moves.

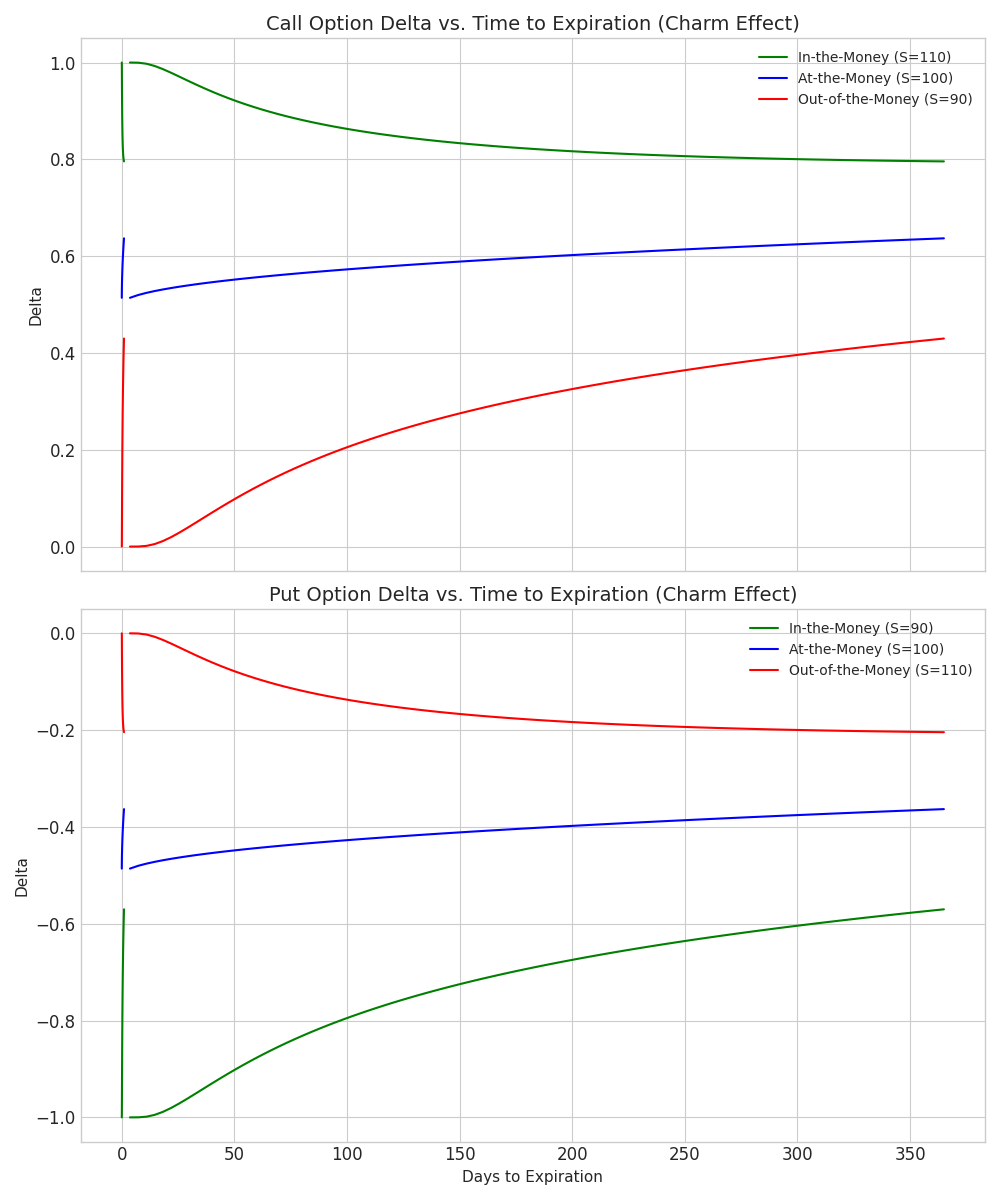
• Charm: Charm is the options Greek that specifically quantifies how Delta itself changes as time passes. Although Charm isn't generally measured, it's useful to understand how Delta moves over time. Out-of-the-money (OTM) options and In-the-money (ITM) options typically have stronger Charm. This means their Deltas decay more quickly towards zero (for OTM) or strengthen more quickly towards 100 (for ITM). At-the-money (ATM) options generally have weaker Charm, meaning their Deltas tend to remain more stable for a longer period.