How to Trade using the Expected Move

If you value statistics and probabilities in your options trading, understanding and using the Expected Move should be a foundation of your trading plan. The Expected Move represents the market defined range of stock movement over a timeframe.

Look at it this way, The expected move is a practical representation of the Implied Volatility, defining what the IV number actually represents on the potential move of an asset. (I hope you're already refering to the Implied Volatility before trading options).

Often shown as a +/- value, or shown in a Volatility Cone, the expected move can provide a guide to assess how far, up or down, the market expects an asset to move by a certain time. This is a reflection of the underlyings Implied Volatility.

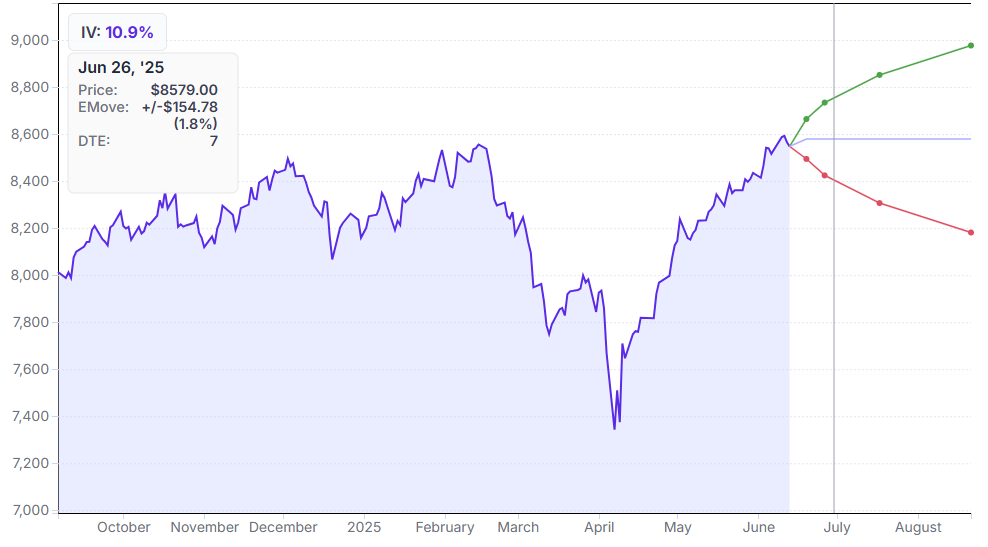
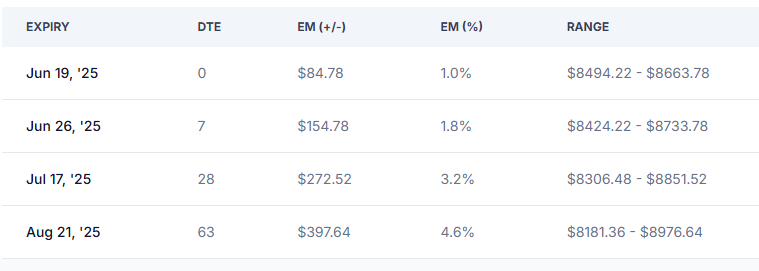
Generally calculated as the premium of the at-the-money Straddle of an asset, it derives usually very close to the 1 Standard Deviation. Where this differs is that:

The Standard Deviation uses the Implied Volatility of the asset - which is calculated at a 30 day period.

The ATM Options can have different Implied Volatility profiles depending on how close to expiration the expiry date is, as shorter term options generally have higher Implied Volatility. Also supply/demand, Market maker hedging or volatility skew can also affect these prices.

Regardless of the differences, if you needed to calculate the Expected Move, the 1 Standard Deviation does a fairly good job and in theory, using THEO prices, they are the very close to the same.

Application

Remeber that the volatility cone is derived from the Implied Volatility quoted from the underlying asset, meaning that the IV Rank is still important and options volatility rules apply, sell High IV and buy Low IV.

Also note that the math included isn't taking into account that Implied Volatility is generally overstated in the market. Studies show that the market applies "Risk premium" to Options and Implied Volatility to account for extreme moves. Studies show that 1 SD is observed from up to 70-80% probabilities for some listed assets.

Selling a put at the 1 Standard Deviation value is a 84% probability of expiring worthless

You read that right. Expiring worthless.. Once you include the premium you receive, the probability of profit is even greater.

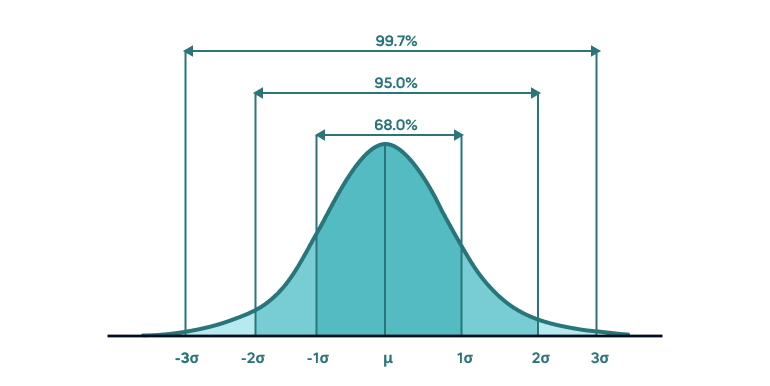
The Math is simple. We know the 1SD range has a 68% probability. This means there is a 32% chance the stock will finish outside this range (16% above, 16% below). If you flip that, it means selling a put option at the bottom of the Expected Move range has an 84% probability of expiring worthless (100% - 16%). Add on your premium received and P.O.P is even greater.

If you're wanting to be more agressive, structure your sold put inside the Expected Move to where your break-even price is at the expected move range, creating a 84% Probability of Profit, but more premium.

The same logic applies to credit spreads. Many traders will use the 1 SD as a reference for the sold leg

Setting up Strangles and Iron Condors

The expected move can also be used as a reference for delta neutral trades like Strangles and Iron Condors to provide that key 68% chance of the strategy expiring worthless; and an ever better chance of profit, by collecting premiums.

Setting up a strangle would include selling a put option at 1SD below the market and selling a call option 1SD above the market.

The Calendar Spread

The Expected Move is dynamic; it expands as you go further out in time. A 30-day EM will be much smaller than a 60-day EM for the same stock. We can explore this "term structure" of volatility with a calendar spread.

Example: Rio Tinto (RIO) .

• Front-Month (30-day expiry): The EM is +/- $6.00. You could sell a strangle at this range.
• Back-Month (60-day expiry): The EM is +/- $10.00. Buying the +/- $6.00 strangle puts you inside the EM, with the opportunity for long options to gain value even within the EM.

The Bottom Line

The Expected Move is far more than a statistic. It is a strategic framework. It allows you to quantify risk, identify high-probability trades, and structure strategies with a clear statistical edge.